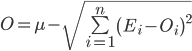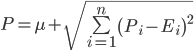Статистический анализ проектных оценок
| April 26, 2012 | Posted by admin under Практики, Статьи |
Версия 3.0
Автор: Евгений Неделько
В своей работе мне постоянно приходится делать оценки для проектов, задач и работ, которые еще только предстоит выполнить, и поэтому точно измерить их невозможно. Недавно один из крупных клиентов Аксенчер, обратился в нашу компанию с просьбой помочь в разработке более систематизированной методики подготовки таких оценок. Проект так и не случился, но материалы, которые я собрал, оказались чрезвычайно полезными для меня самого. Возможно, они заинтересуют вас тоже.
Первое, что я сделал, когда подключился к этому проекту, – я постараться сформулировать суть проблемы, то есть задачу, которую я хочу решить. Почти во всех проектах, в которые я был вовлечен, план строился на точных оценках отдельных задач, на конкретных числах указанных в качестве продолжительности, трудоемкости или стоимости задачи. Лишь некоторые проекты использовали методику PERT, определяя кроме наиболее ожидаемых затрат также оптимистичные и пессимистичные оценки, но даже в этом случае общая оценка проекта представляла собой одно конкретное число. Я же понимал, что в реальности фактические затраты всегда будут больше или меньше первоначальной оценки, а вероятность точного совпадения стремится к нулю. Я был уверен, что любой выделенный бюджет будет или перерасходован, или недотрачен. Нашему потенциальному клиенту и мне лично хотелось получить возможность определять вероятность вписаться в тот или иной бюджет, т.е. с одной стороны избежать ситуации, когда деньги кончаются посреди проекта, а с другой стороны избежать ситуации, когда остаются лишние деньги, которые просто «осваиваются», не принося уже дополнительных прибылей бизнесу.
И тут мне повезло: наша компания, являясь одним из крупнейших в мире поставщиков услуг в области аутсорсинга, обладает огромными массивами данных по выполненным проектам, и я смог довольно быстро получить большую выборку данных от одного из Российских проектов. Я получил значения оценок и фактических затрат по нескольким тысяч заявок с типичными трудозатратами от 1 до 50 ч-часов. После несложных манипуляций в Excel я получил искомое распределение (рис. 1). На гистограмме по вертикали отложено число заявок, а по горизонтали – размер фактических затрат относительно прогнозируемых. Например, если фактические затраты совпадают с оценкой, то на гистограмме такая заявка увеличит на единицу столбик в точке 1. Если фактические затраты составили полдня при оценке в два дня, то заявка попадет в точку 0,25.
Рис.1. Распределение фактических затрат в одном проекте
Вот что то я увидел анализируя получившийся график:
Во-первых, оказалось что наши сотрудники делают очень правдоподобные оценки, т.е. указывают те затраты, вероятность которых максимальна (на графике эта точка отмечена зеленым цветом). Если наш специалист говорит, что какая то задача займет 12 часов, то вероятность того, что задача займет именно 12 часов немного выше вероятности того, что реальные затраты составят 11 или 13 часов, и намного выше того, что затраты будут равны 6 или 24 часам.
Во-вторых, когда я подсчитал средние затраты по всем заявкам, то обнаружил, что среднее арифметическое оказались заметно больше, чем первоначальные оценки. В первый год работы проекта средние затраты превышали исходную оценку на 50%, потом разница сократилась до 30%, но никуда не исчезла. Этому странному на первый взгляд факту нашлось простое объяснение. Ошибиться в сторону уменьшения затрат мы можем не больше, чем на первоначальную оценку (размер затрат ведь не может быть отрицательным), а в сторону превышения оценки у нас нет почти никаких ограничений и фактические затраты могут превысить оценку в два, в три, в четыре или даже в десять раз. Примеры, к сожалению, имеются. В результате ошибки в сторону увеличения затрат перевешивают ошибки в сторону уменьшения, и в среднем реальные затраты оказываются больше самых правдоподобных и вероятных оценок. Говоря языком статистики, получается, что распределение фактических затрат несимметрично, а математическое ожидание больше моды распределения.
Следующим важным наблюдением является поведение людей, которые гарантируют, что они впишутся в обещанные затраты. Для того чтобы быть уверенными в этом они подписываются под той оценкой затрат, риск превысить которую не больше 5-10%. А это означает, что вероятность того, что реальные затраты составят меньше обещанного – 90-95%, причем судя по полученному распределению – превысят раза в 2-3. Получается, что гарантированное соблюдение бюджета и сроков выливается в 2-3 кратное увеличение бюджета и сроков, т.е. строгий контроль сроков и бюджетов без оглядки на их адекватность и реалистичностьгарантирует падение общей эффективности.
Чтобы побороться с этим эффектом некоторые заказчики и руководители требуют указания в качестве целевых наиболее вероятных оценок затрат и соглашаются прощать возможное превышение оценок в рамках резервов на непредвиденные обстоятельства. К сожалению, размер таких резервов редко когда превышает 20%, а как я написал выше, затраты по отдельным задачам в среднем превышают правдоподобные оценки на 30-50%. В рамках большого проекта ошибки по отдельным задачам могут компенсировать друг друга, но, тем не менее, со временем ошибки накапливаются и приводят к гарантированному превышению целевого бюджета.
Чтобы побороть этот пагубный эффект можно воспользоваться одним из двух методов: можно попытаться рассчитать поправочный коэффициент к сумме правдоподобных оценок, или воспользоваться методикой PERT, разработанной еще в 50-е годы прошлого века на основе идей Генри Форда и Фредерика Тейлора. Первый способ — проще, однако второй позволяет не только получить реалистичную оценку, но и понять каково распределение возможных значений фактических затрат.
***
Для того чтобы рассчитать реалистичную оценку на базе наиболее правдоподобной, используя поправочный коэффициент, этот коэффициент для начала нужно рассчитать. Для этого нужно взять не менее 20-40 выполненных задач и рассчитать среднее отношение фактических затрат к исходной оценке. Если размеры оценок различаются более чем в два-три раза, то имеет смысл определить два или даже больше коэффициентов для задач разных размеров. В использованных мной данных, поправочный коэффициент для задач с оценкой менее 2 ч-часов оказался в три раза больше коэффициента для задач с оценкой от 12 до 24 ч-часов.
После того как получен набор поправочных коэффициентов, необходимо умножить каждую правдоподобную оценку на соответствующий поправочный коэффициент, а полученные произведения просуммировать. В результате получится реалистичная оценка затрат по проекту, для которой риск поставщика превысить бюджет равен риску заказчика заплатить лишнее.
Недостатком этого метода является сильная зависимость результата от аккуратности расчета поправочного коэффициента, поэтому большинство методологий Agile использующих данный метод, требуют уточнения поправочного коэффициента после каждой итерации или релиза. Кроме того эти методологии стимулируют разбивать работу на задачи примерно одинакового размера, что позволяет обходиться всего одним коэффициентом.
***
Методика PERT в отличие от предыдущего метода не использует никаких предопределенных коэффициентов и использует несколько оценок по каждой задаче для расчета реалистичной оценки всего проекта.
Для того, чтобы рассчитать реалистичную оценку проекта по методике PERT необходимо указать для каждой задачи три оценки: полученную обычным способом наиболее правдоподобную оценку, оптимистичную – оценив минимальные затраты в случае, если мы переоцениваем сложность задачи, и пессимистичную – оценив максимальные затраты, которые могут потребоваться для завершения задачи. После чего реалистичная оценка по отдельной задаче определяется по представленной ниже формуле. Затраты по всему проекту в целом оцениваются простым суммированием реалистичных оценок по каждой задаче.
где
μ – реалистичная оценка затрат по проекту или релизу в целом,
n – число задач в проекте или релизе,
μi – реалистичная оценка затрат по задаче i,
Oi – оптимистичная оценка затрат по задаче i,
Ei – наиболее правдоподобная оценка затрат по задаче i,
Pi – пессимистичная оценка затрат по задаче i
Тут важно обратить внимание на ещё одну особенность полученных данных — вероятность ошибиться в два раза в сторону уменьшения оказалось равной вероятности ошибиться в два раза в сторону увеличения. Т.е. распределение относительной ошибки (в отличие от абсолютной ошибки) оказалось симметричным. Соответственно соотношение наиболее правдоподобной оценки к оптимистичной должно быть минимально отличаться или равно отношению пессимистичной оценки затрат к наиболее правдоподобной оценке.
Если это не так, то имеет смысл проверить правильность оптимистичной и пессимистичной оценок.
***
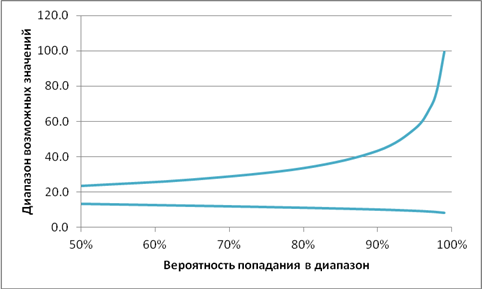
Для определения необходимых резервов на непредвиденные нужды требуется рассчитать интервал возможных затрат при заданной оценке (см. рис.2). Если первоначальная оценка по задаче составила 16 ч-часов, то с 50% вероятностью можно говорить о том, что фактические затраты будут находиться в диапазоне от 15 до 24 ч-часов, а с вероятностью 95% можно было утверждать лишь то, что затраты будут в диапазоне от 3 до 56 ч-часов.
Рис 2. Доверительный интервал
Наиболее типичным является использования диапазона с вероятностью 90%. В этом случае предполагается вероятности того, что значение затрат превысит пессимистичную оценку, и того, что затраты окажутся меньше оптимистичной оценки, равны по 5%. Вероятность того, что фактические затраты попадут в диапазон между оптимистичной и пессимистичной оценкой равна 90%.
Получение распределения вероятностей фактических затрат по релизу и проекту возможно используя оптимистичные и пессимистичные оценки полученные в методике PERT. Сама методика для получения диапазона возможных значений предлагает просто сложить оптимистичные и пессимистичные оценки, однако простейшее моделирование показывает, что это некорректно. Пессимистичная оценка проекта оказывается меньше суммы оценок, а оптимистичная – больше. Диапазон с вероятностью 90% оказывается меньше простой суммы диапазонов для отдельных задач.
Точной формулы для вычисления нужного нам диапазона случайно распределенных величин не существует, однако хорошее приближение дает следующая формула, говорящая о том, что разброс возможных значений затрат растет пропорционально квадратному корню от числа задач в проекте или релизе:
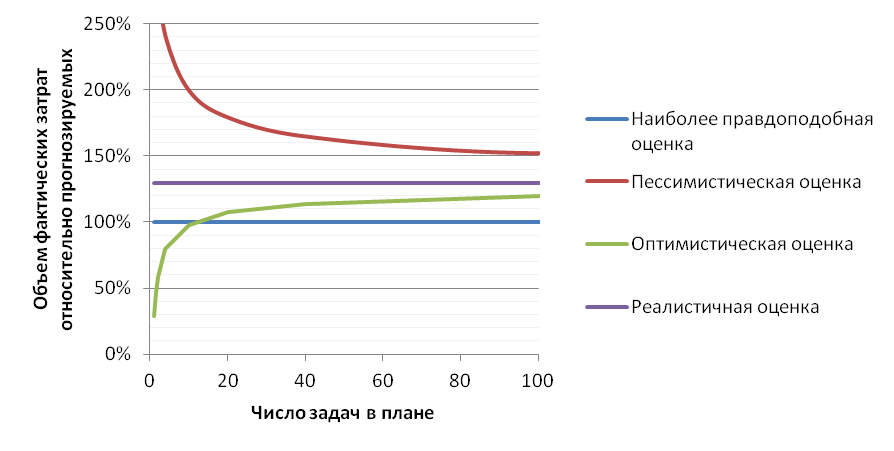
Соответственно, чем детальнее мы разбиваем большой проект и больше задумываемся о каждой отдельной задаче, тем более точную оценку мы можем дать. Например, если взять большой интеграционный проект внедрения, трудозатраты по которому могут составить 50 000 ч-дней, то разбив план на 1 000 задач мытеоретически можем получить погрешность менее 800 ч-дней или менее 2%. График теоретической зависимости разброса затрат в зависимости от детальности плана представлен на рис.3.
Рис.3. Теоретическая зависимость точности оценки затрат в зависимости от количества подзадач в плане:
К сожалению, в реальной жизни есть ряд ограничений не позволяющих достигнуть такой точности и самым существенным является то, что требования и состав выполняемых задач может меняться по ходу проекта. Для большинства компаний типичным является потеря актуальности 10-30% задач, поэтому как бы мы не детализировали наш план, ошибка в первоначальных оценках всё равно неизбежна.
Суммируя полученные выводы, мне удалось понять следующее. Используя для оценки большого проекта сумму наиболее правдоподобных оценок затрат, мы гарантировано занижаем оценку, суммируя пессимистичные оценки – гарантировано её завышаем. Для того, чтобы получить реалистичную оценку необходимо использовать предварительно рассчитанный поправочный коэффициент или методику оценки ПЕРТ. Воспользовавшись оценками в методике ПЕРТ мы также можем получить диапазон затрат, про который можно говорить, что фактические затраты попадут в него с вероятностью 90% и в котором нет излишних резервов. А детализируя план проекта и аккуратно оценивая каждую задачу, можно существенно сократить этот диапазон, в итоге достигая требуемого размера резервов.
Евгений Неделько
Менеджер практики совершенствования ИТ процессов компании Accenture
-
Dan Gonchar